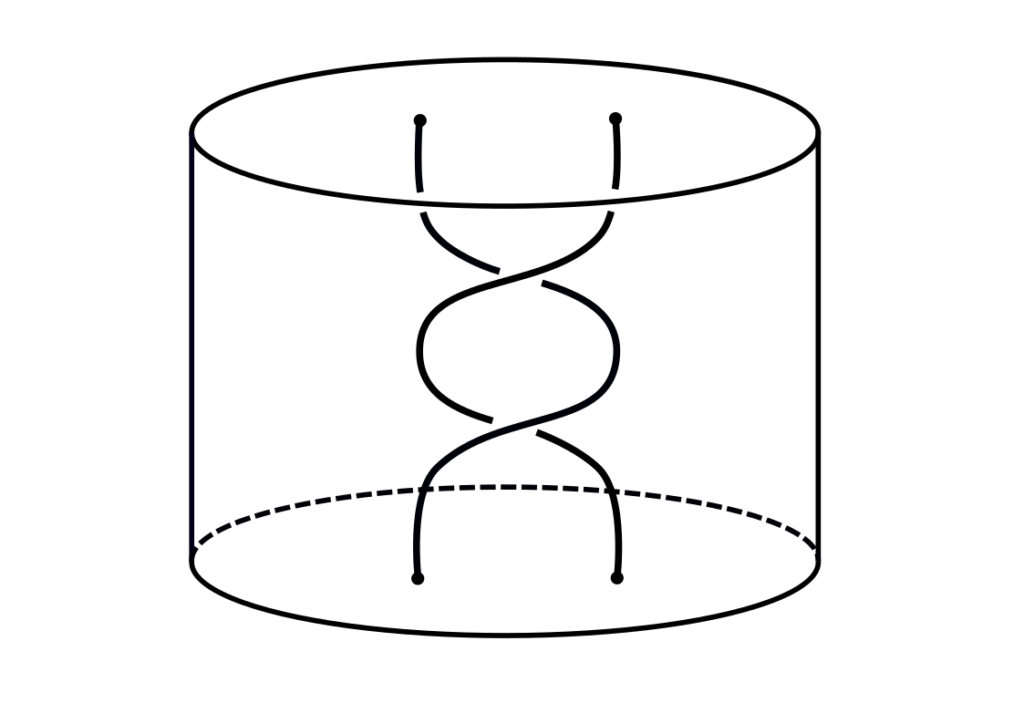Research

I am interested in string link infection, string link operators, and the maps they induce on concordance groups.

A string link can be thought of as an embedding of m disjoint intervals into a thickened disk so that the i th endpoint at the top is connected to the i th endpoint at the bottom.

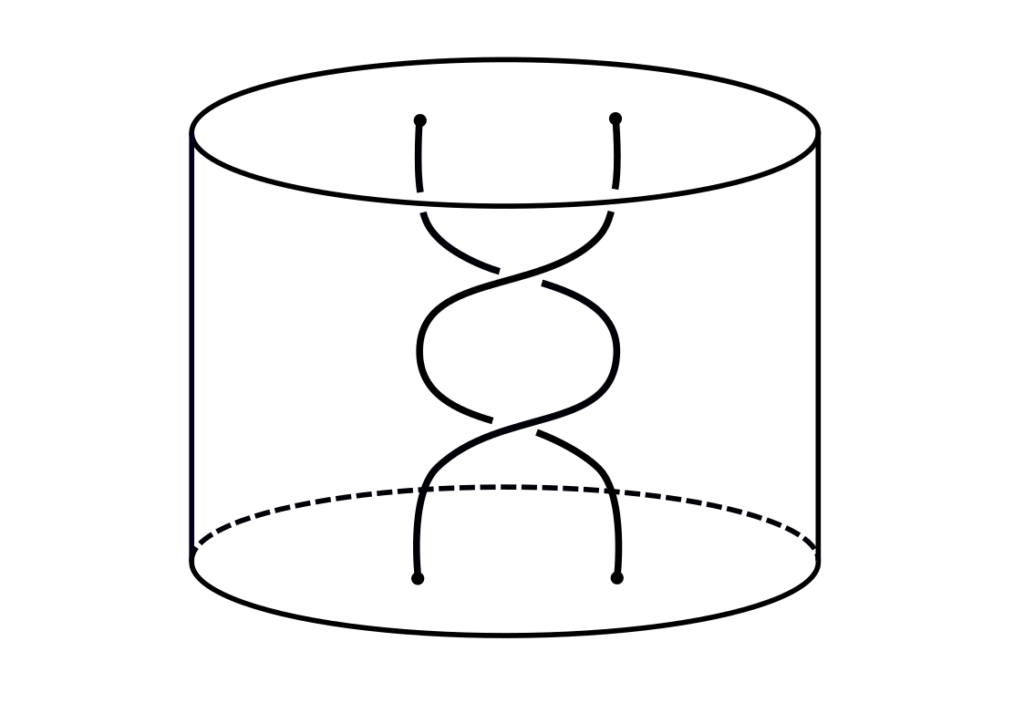
Given a knot K, an embedded disk D that intersects K only in m disjoint subdisks, and an m-component string link L, we can infect K by the string link L along D by tying the strands intersecting the subdisks in the pattern of L. The following images illustrate first R and D, then L, and finally infection of R by L along D.

If we fix the knot K and the disk D, which we call a pattern, we can consider them as an operator from the set of m-component string links to the set of knots. This induces a map from the m-component string link concordance group to the knot concordance group. My research focuses on the the use of concordance invariants to study properties of these maps.

Talks

• GTA: Philadelphia, Temple University, May 2022
  • A Hedden-Style Conjecture for String Links
  • A copy of my abstract is available through the link.
• JMM, Virtual, April 2022
  • A Hedden Style Conjecture for String Links
  • A recording of the talk is available through the link.
• Topology et. al. Seminar, Wesleyan University, Feb. 2020
  • The Slice-Ribbon Conjecture
• Graduate Student Seminar, Wesleyan University
  • Rational Tangles and 2-Bridge Knots, Spring 2022
  • A Hedden-Style Conjecture for String Links, Fall 2021
  • The Slice-Ribbon Conjecture, Spring 2020
  • The Classical Concordance Group, Fall 2019
  • Slice Knots and Concordance, Spring 2019
  • Cyclic Covers and Torsion Invariants, Fall 2018

Conferences

• GTA: Philadelphia, Temple University, May 2022
• JMM, Virtual, April 2022
• GSTGC, Virtual, April 2021
• NCNGT, Virtual, May 2020
• Tech Topology Conference, Georgia Tech, Dec. 2019
• UnKnot IV, University of Washington Bothell, July 2019